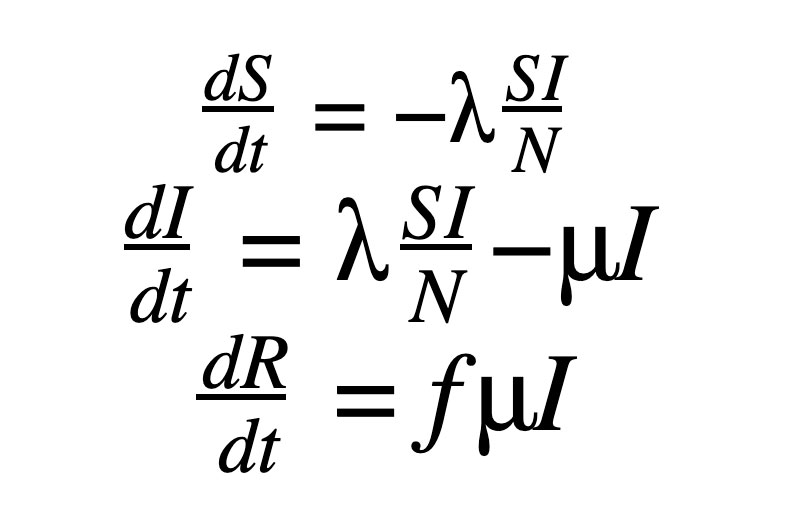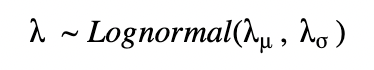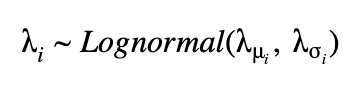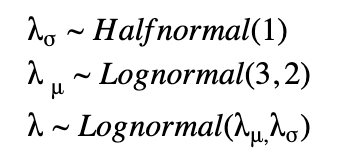ベイズ階層モデルによる COVID-19 疾患パラメタの推定

前のブログでは、COVID-19（新型コロナウイルス感染症）疾患のダイナミクスを PyMC3 でモデル化する方法を解説しました。今回は、同じユースケースを使用して、ベイズ階層モデルによる COVID-19 疾患パラメタの推論方法および、プールモデル／非プールモデルと比較した場合のメリットについて、次のような順序で解説します。
1) SIR モデルを常微分方程式（ODE）で生成した合成データに当てはめ、R₀ などの疾患パラメタを推論する。
2) 上記のフレームワークを実際のデータセット（国ごとの 1 日あたりの感染者数）に適用する。
3) このモデルの限界を指摘し、推論プロセスを改善する方法を考察する。

なお、Coursera の専門講座「Introduction to Computational Statistics for Data Scientists Specialization」（データサイエンティストのための計算統計学）を開設しました。この講座のコース 2 と 3 で、このブログの内容と関連するベイズモデルと推論について解説しています。

SIR モデル

COVID-19 をモデル化した前回の投稿で説明したように、SIR モデルには 3 つの常微分方程式（ODE）が含まれており、S（Susceptible）、I（Infected）、R （Recovered）の 3 つのコンパートメントがあります。

ここで、S は感染症への免疫のない人、I は現在感染している人、R は感染から回復して免疫がある人を指しており、総人口 N と合わせて以下が成り立ちます。

 

S + I + R = N
 

ここでは、疾患から一度回復すれば、生涯免疫が獲得されることを前提にしています。しかし、このような前提が当てはまらない疾患も多くあるため、有効なモデルとはならない場合もあります。

λ は感染率、μ は疾患からの回復率です。感染後に回復する人の割合は f で示されますが、今回は便宜上、 f を 1 に設定しています。最終的には、上記の ODE における初期値問題（IVP）となりますが、I(0) はパンデミック開始時の症例数から把握できると仮定すると、S(0) は N - I(0) で推定できます。そして、全人口が感染していないと仮定したうえで、以下を達成することが目標です。

• ベイズ推論を用いて、λ と μ を推定する。
• 上記のパラメタを用いて、任意の時刻 t における I(t) を推定する。
• R₀ を計算する。

プールモデル、非プールモデル、階層モデル

アメリカの各州の感染者数に関する情報があるとします。このデータを使って COVID-19 の疾患パラメタ（R₀ 等）を推測する場合、まず、全てのデータを合計して 1 つのパラメタを導き出す方法があります。これを「プールモデル」と呼びます。しかし、この方法では、個々の州やグループ内の細かい情報が欠落する可能性があります。逆に、州ごとに個別にパラメタ R₀ を推定する方法も適用できます。これが「非プールモデル」です。しかし、どちらも同じウイルスに関するパラメタを推定したいため、これらをまとめて行う方法が必要です。これが、「階層モデル」です。この方法は、特定の州で十分な情報が得られず、正確な推定値が得られない場合に特に有効です。階層モデルでは、hyperprior（超事前分布）を共有することで、他の州の情報を共有できます。具体的に λ について式で詳しく見てみましょう。

プールモデルの場合は、固定パラメタ λ_μ、λ_σ を持つ単一の分布から λ を求めることができます。

非プールモデルの場合は、固定パラメタ λ_μ、λ_σ からそれぞれについて λ を求められます。

階層モデルにおいては、他の分布から導き出された非定数のパラメタを使ってパラメタ化された事前分布が用意されます。それぞれの州ごとに λ が求められますが、下に示すように、超事前分布の共有を通じて、それらが関連するようになっています。

Coursera 専門講座のコース 3 「Introduction to PyMC3 for Bayesian Modeling and Inference」（ベイズモデリングと推論のための PyMC3 入門）で詳しく解説しています。

合成データを用いた階層モデル

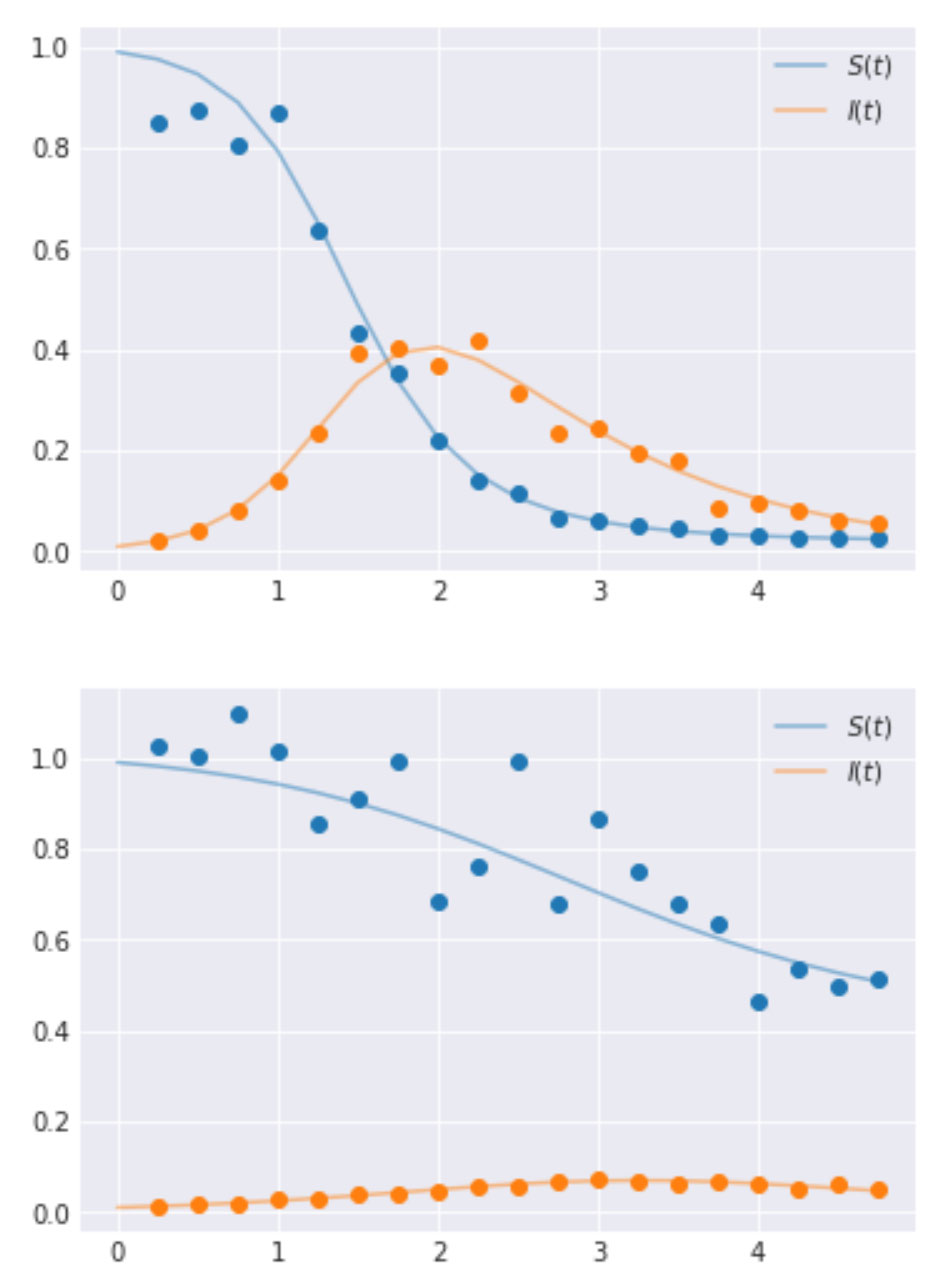
階層モデルの実装と、その詳細について説明するために、SIR モデルを定義する ODE を使用してデータを生成します。これらの値は、あらかじめ設定された時間ステップで生成されます。今回は時間間隔を 0.25 としました。また、説明しやすいようにグループを 2 つ選択していますが、グループは必要に応じていくつでも作成できます。λ と μ の値は、2 つのグループでそれぞれ [4.0, 3.0] と [1.0, 2.0] に設定しました。以下に、生成コードと出力される時系列曲線を示します。

合成データの生成

 

階層モデルによる推論の実行

 

COVID-19 に関する実データ

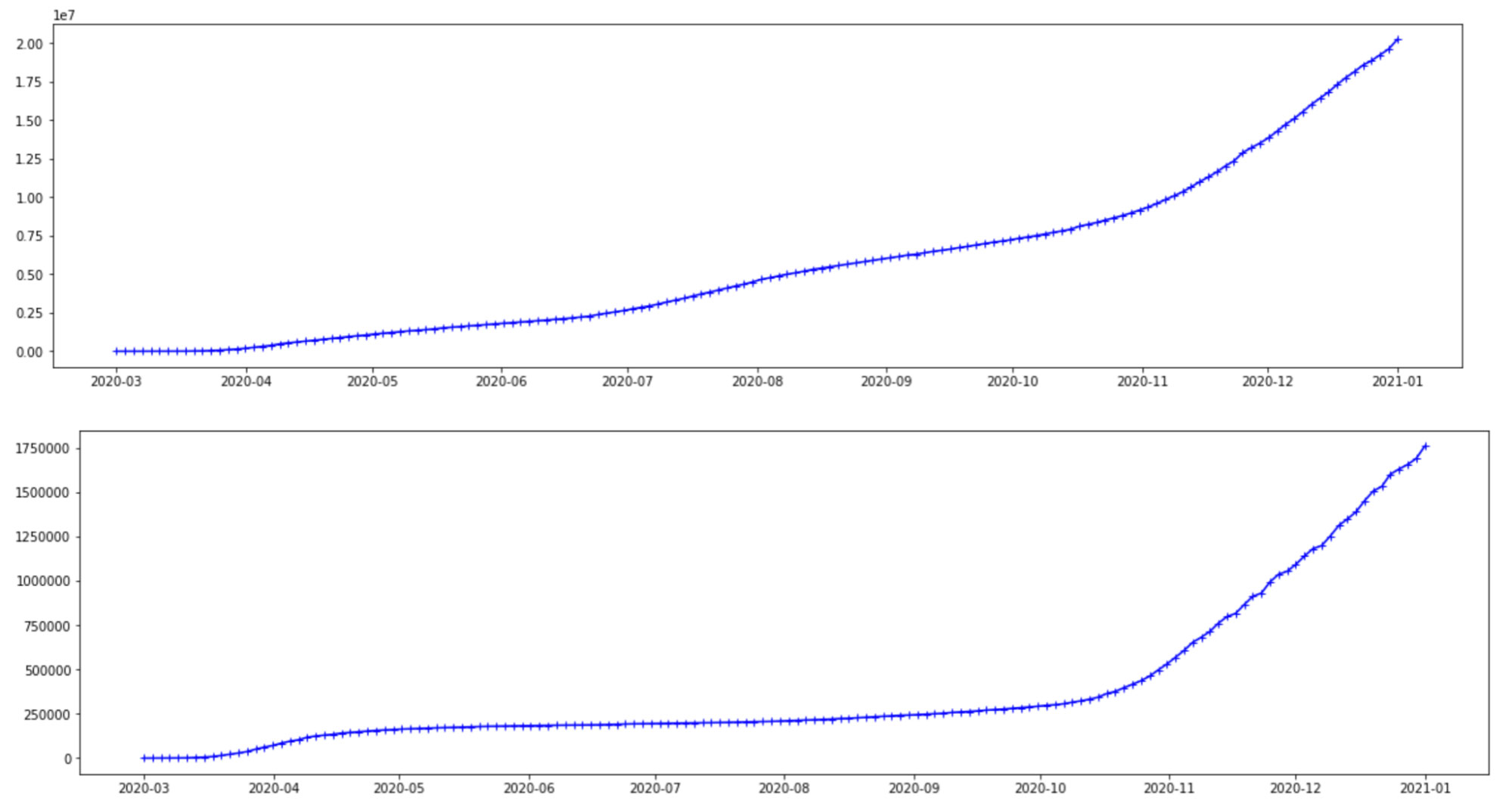
ここで使用するデータは、症例数が定期的に更新されているジョンズ・ホプキンス大学システム科学工学センター（CSSE）の Github ページから取得しています。アメリカとブラジル、2 か国の 1 日あたりの感染者数をプロットして使用しました。今回は 2 か国を対象にしましたが、階層モデルでは、使用する国やその数に制限はありません。下のグラフで示しているのは、2020 年 3月 1 日から 2021 年 1 月 1 日までのデータです。Y 軸の目盛りは異なりますが、両国で同じような推移をたどっているように見えます。いずれも同じ COVID-19 ウイルスに関するデータであることを考えれば、妥当なことです。しかし、変異株の種類、地理的な特徴、ソーシャルディスタンスのルールや医療インフラなど、考慮すべき違いが存在しています。

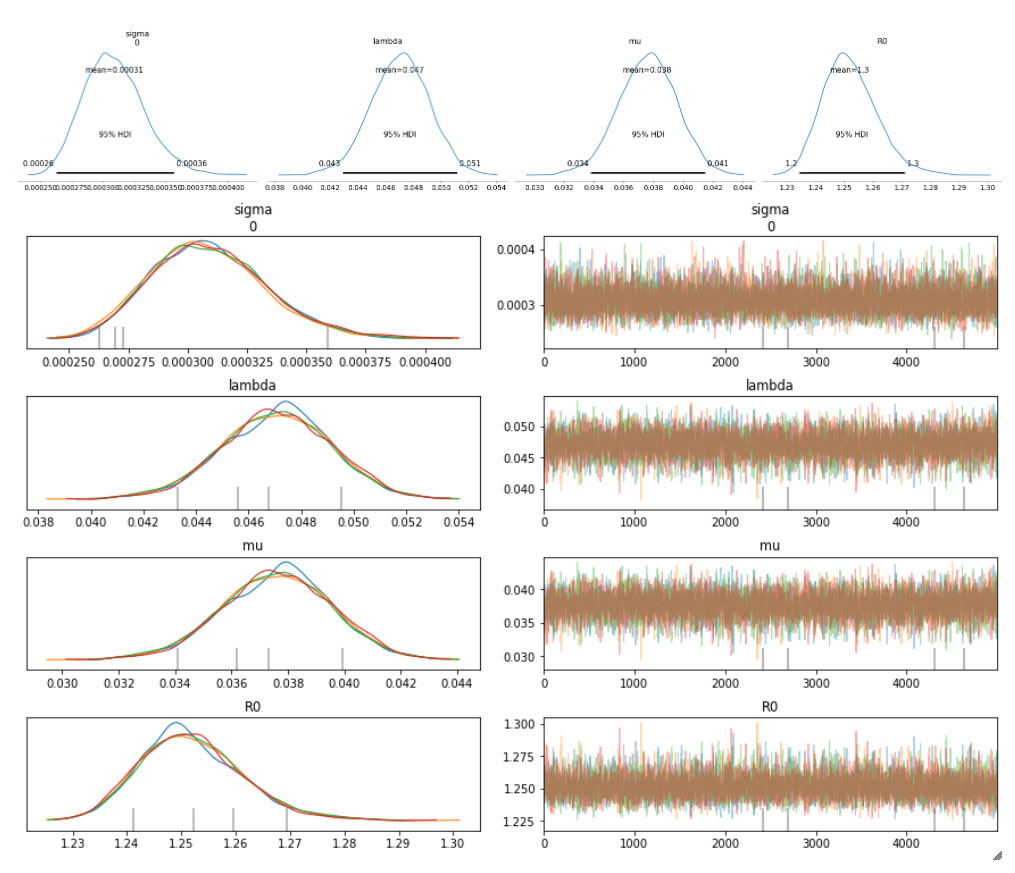
パラメタの推論

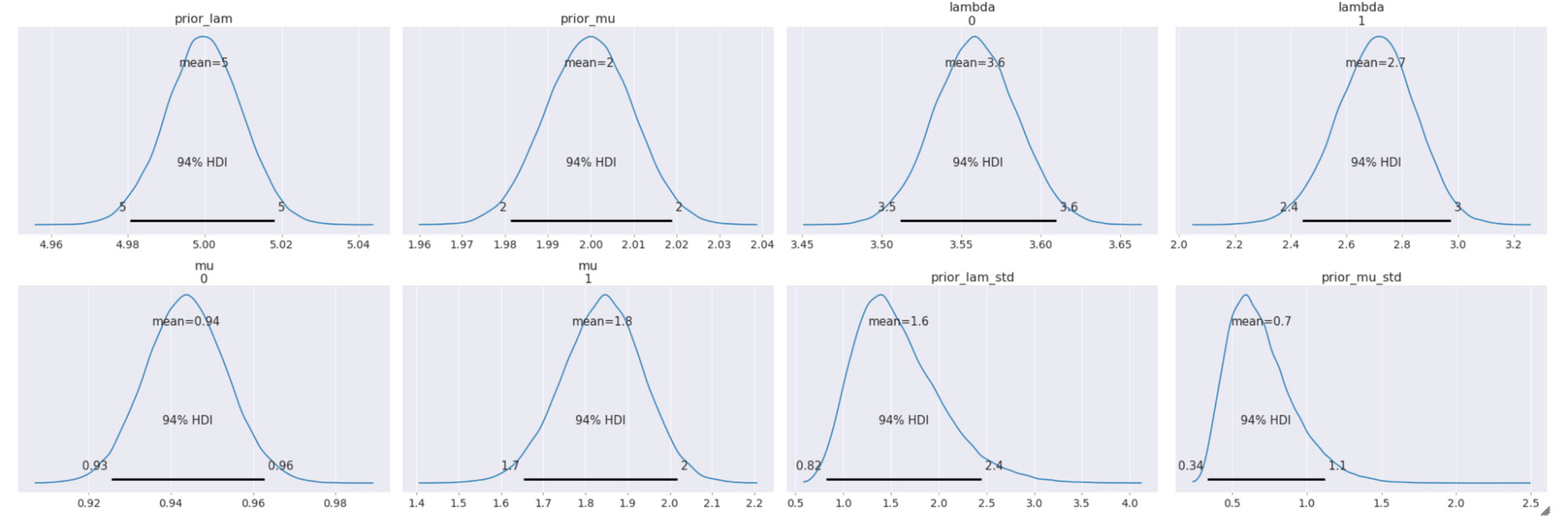
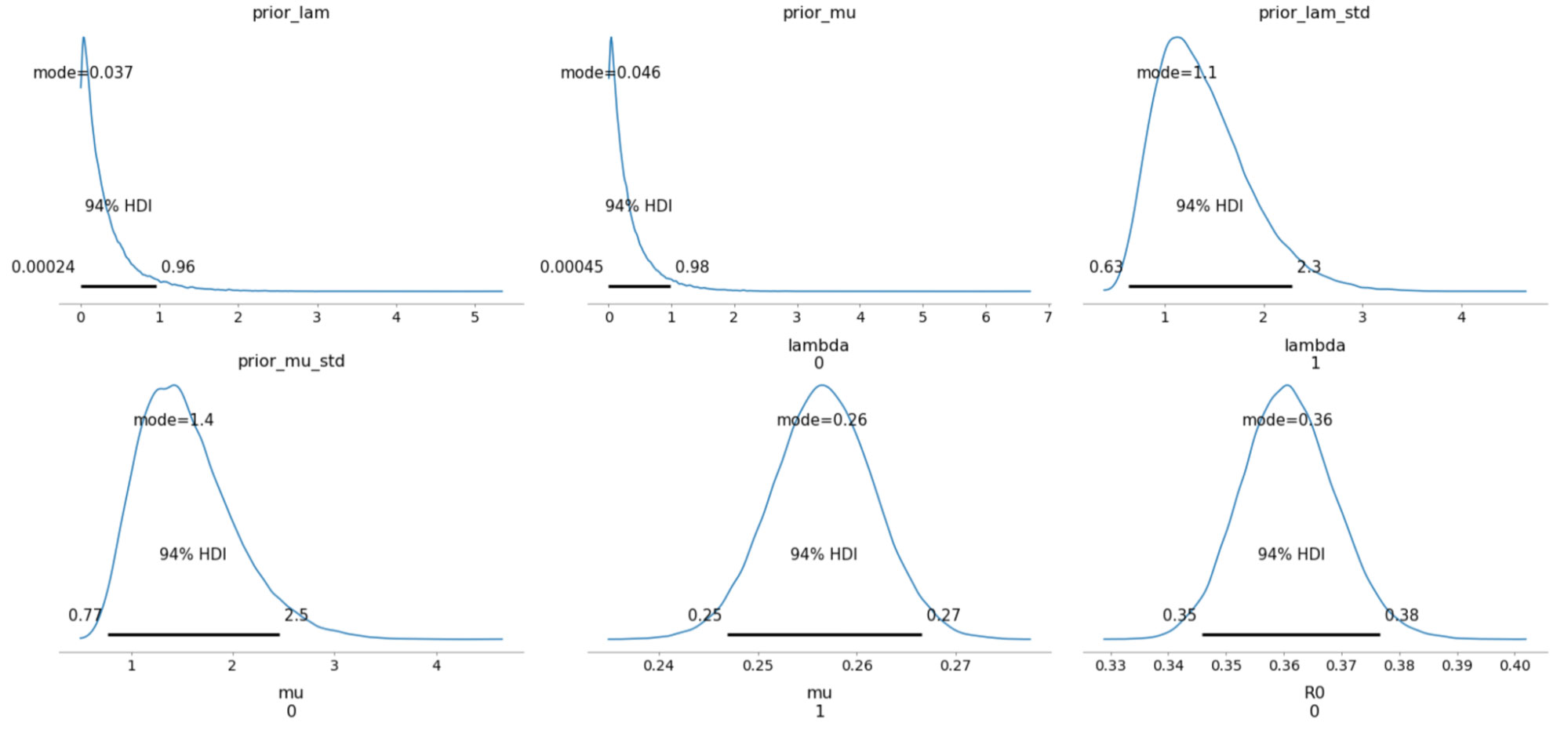
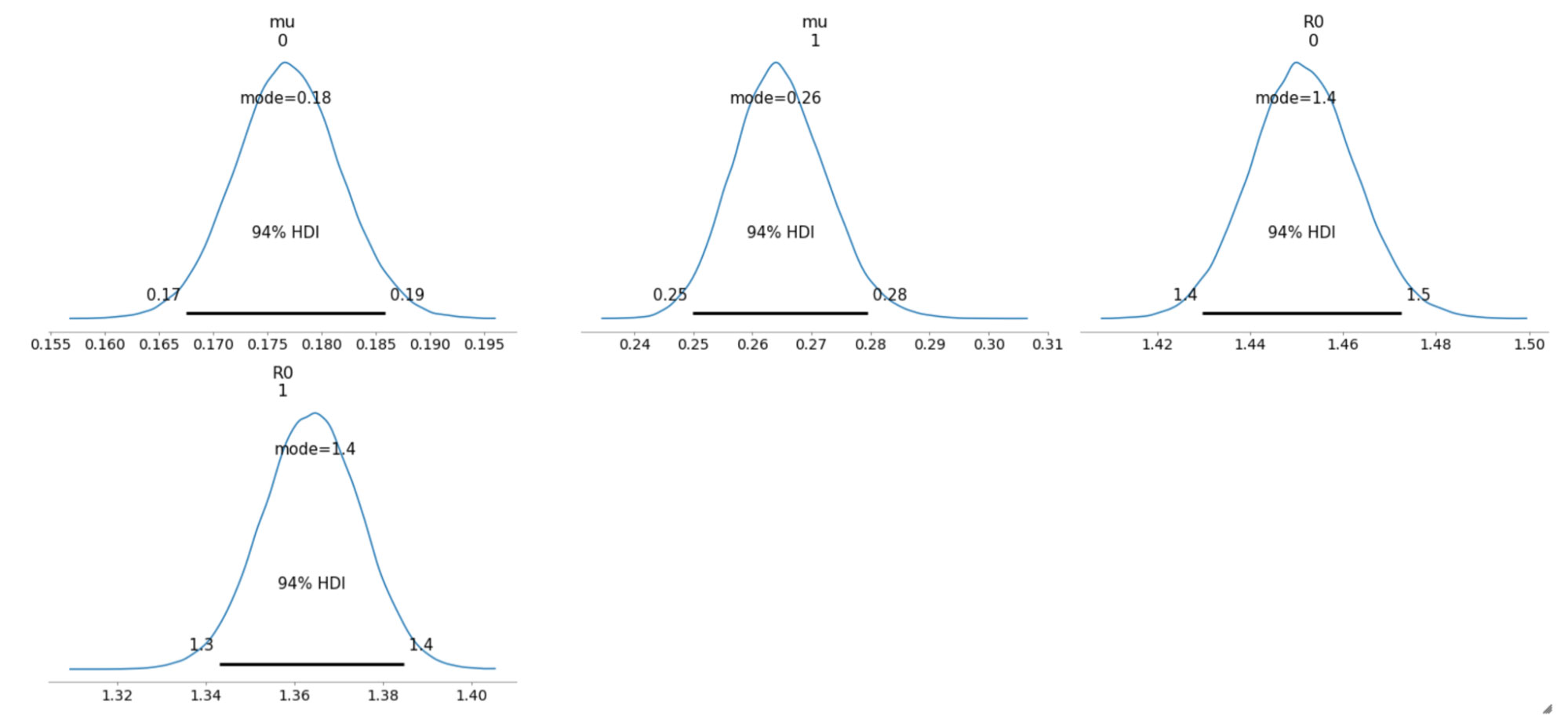
以下は、サンプリングされた事後分布について、94% 最高密度区間（HDI）で示したものです。

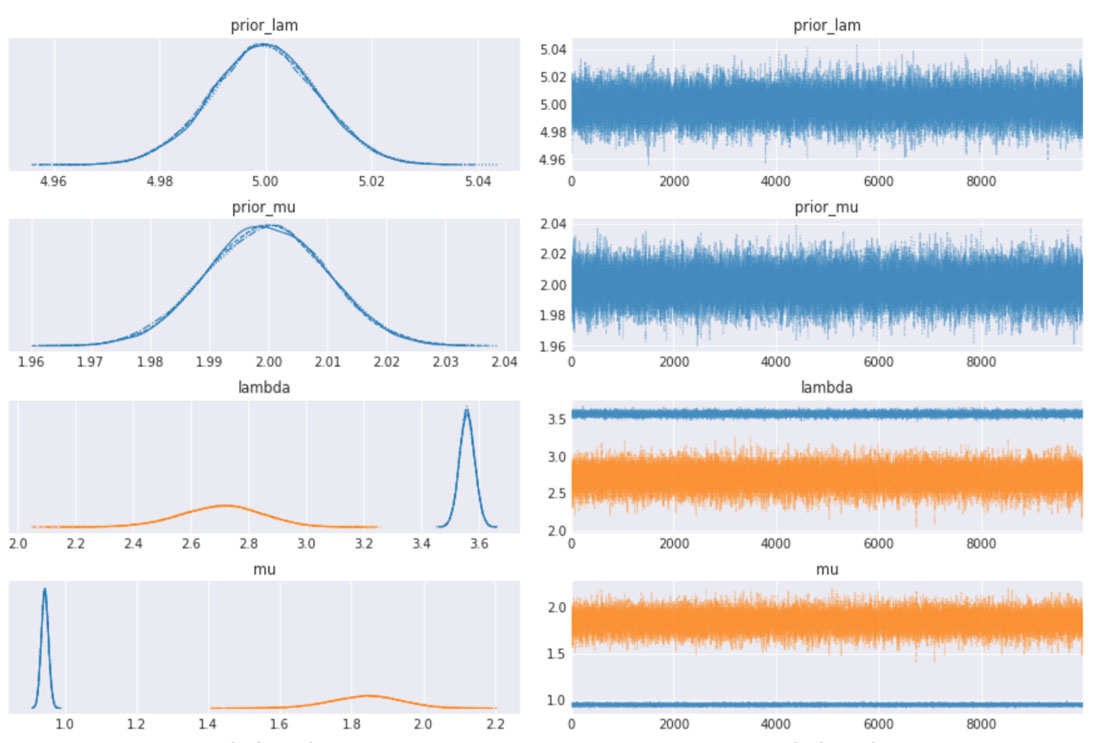
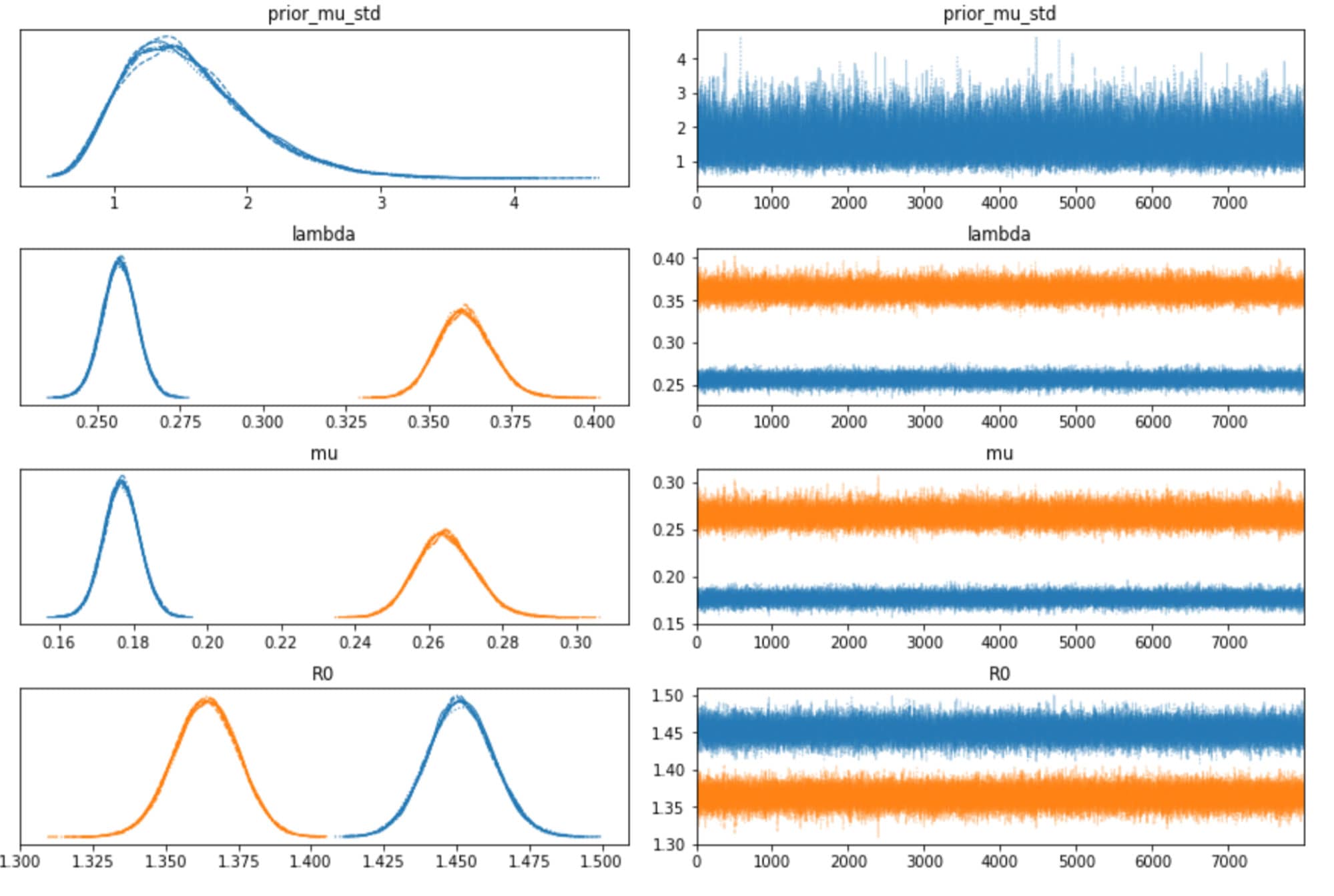
収束についてトレースプロットも確認しましたが、全ての変数でうまく混合しており、サンプラーで十分に空間が探索されたことがわかります。各トレース間にも十分な一致がみられます。これは上記のプロットの HDI 間隔が極めて狭いことからも確認できます。

 

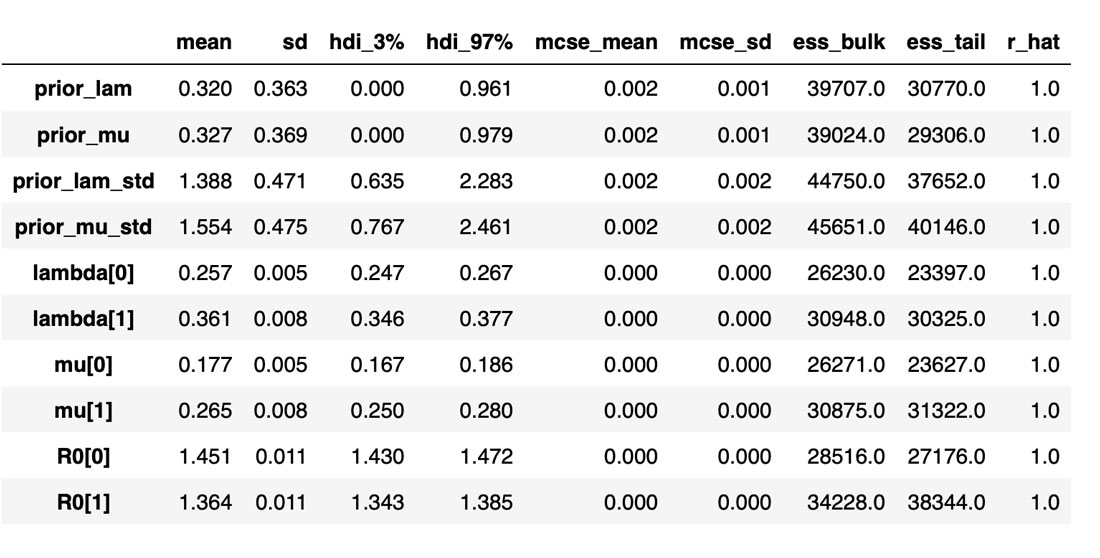
下の表は、推測されるさまざまな変数やパラメタの分布と、サンプラーの統計値をまとめたものです。変数に関する推定値が必須ですが、この表は特にサンプラーの質と効率を把握するのに役立ちます。例えば、Rhat が全て 1 に等しくなっており、全てのチェーンで十分な一致がみられることを示しています。有効なサンプルサイズも重要な指標です。全体のサンプル数よりも少なければ、サンプラーに問題があると考えてよいでしょう。Rhat の値が良さそうに見えても、必ず有効なサンプルサイズを確認するようにしてください。

これでパラメタの推定値は十分なものになりましたが、サンプラーが有効に機能しないという問題が発生することもあります。このシリーズの次のブログ投稿では、問題の診断を行い、モデリングプロセスを改善する方法をみていきます。内容は、難易度の低いものから順に、以下のとおりです。

1. チューニングサイズとサンプル数を増やす。
2. サンプラーの target_accept パラメタを減らし、サンプル間の自己相関を縮小する。確認には自己相関プロットを使用する。
3. 観測されたデータにさらにサンプルを追加し、サンプル頻度を増やす。
4. パラメタの事前分布や超事前分布を改善する。
5. 別の方法でモデルのパラメタ化を行う。
6. ソーシャルディスタンスの方法等の変更をモデルに組み込む。

これらのトピックのさらなる詳細については、Coursera の専門講座で学習できます。この講座は以下の 3 つのコースで構成されています。

1. ベイズ統計学入門
2. MCMC によるベイズ推論 
3. ベイズモデリングと推論のための PyMC3 入門

 

講座の内容を見る