Announcing the TFOCS for Spark Optimization Package

Aaron is the developer of this Apache Spark package, with support from Databricks. Aaron is a freelance software developer with experience in data infrastructure and analytics.
Click-through prediction, shipping logistics, and housing market analysis are just a few of the many applications of mathematical optimization. While the mathematical models for these applications come in a variety of flavors, a common optimization algorithm can often be leveraged under the hood.
With this in mind we are excited to introduce TFOCS for Spark, a community port of the state of the art TFOCS (Templates for First-Order Conic Solvers) package for Matlab. Whereas Matlab TFOCS operates on data within a single machine’s memory, our Apache Spark port leverages the Apache Spark cluster computing framework to scale to larger problems exceeding the memory capacity of a single machine. This package is a general purpose optimization package for constructing and solving mathematical objective functions. It can be used to train many types of machine learning models and to solve other optimization problems including linear programs, often with little or no configuration required.
The name “TFOCS” is being used with permission from the original TFOCS developers, who are not involved in the development of this package and hence not responsible for the support. To report issues or request features about TFOCS for Spark, please use our GitHub issues page.
This blog post presents a technical overview of TFOCS for Spark along with usage examples. While some of the details may not be for the faint of heart, we describe them because TFOCS for Spark will eventually underpin higher level applications accessible to all Spark users. We will also discuss further details of TFOCS for Spark at an upcoming Bay Area Spark Meetup. RSVP now!
TFOCS
TFOCS is a state of the art numeric solver; formally, a first order convex solver. This means that it optimizes functions that have a global minimum without additional local minima, and that it operates by evaluating an objective function, and the gradient of that objective function, at a series of probe points. The key optimization algorithm implemented in TFOCS is Nesterov’s accelerated gradient descent method, an extension of the familiar gradient descent algorithm. In traditional gradient descent, optimization is performed by moving “downhill” along a function gradient from one probe point to the next, iteration after iteration. The accelerated gradient descent algorithm tracks a linear combination of prior probe points, rather than only the most recent point, using a clever technique that greatly improves asymptotic performance.
TFOCS fine tunes the accelerated gradient descent algorithm in several ways to ensure good performance in practice, often with minimal configuration. For example TFOCS supports backtracking line search. Using this technique, the optimizer analyzes the rate of change of an objective function and dynamically adjusts the step size when descending along its gradient. As a result, no explicit step size needs to be provided by the user when running TFOCS.
Matlab TFOCS contains an extensive feature set. While the initial version of TFOCS for Spark implements only a subset of the many possible features, it contains sufficient functionality to solve several interesting problems.
Example: LASSO Regression
A LASSO linear regression problem (otherwise known as L1 regularized least squares regression) can be described and solved easily using TFOCS. Objective functions are provided to TFOCS in three separate parts, which are together referred to as a composite objective function. The complete LASSO objective function can be represented as:
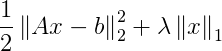
This function is provided to TFOCS in three parts. The first part, the linear component, implements matrix multiplication:
![]()
The next part, the smooth component, implements quadratic loss:
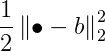
And the final part, the nonsmooth component, implements L1 regularization:
![]()
The TFOCS optimizer is specifically implemented to leverage this separation of a composite objective function into component parts. For example, the optimizer may evaluate the (expensive) linear component and cache the result for later use.
Concretely, in TFOCS for Spark the above LASSO regression problem can be solved as follows:
Here, `SmoothQuad` is the quadratic loss smooth component, `LinopMatrix` is the matrix multiplication linear component, and `ProxL1` is the L1 norm nonsmooth component. The `x0` variable is an initial starting point for gradient descent. TFOCS for Spark also provides a helper function for solving LASSO problems, which can be called as follows:
A complete LASSO example is presented here.
Example: Linear Programming
Solving a linear programming problem requires minimizing a linear objective function subject to a set of linear constraints. TFOCS supports solving smoothed linear programs, which include an approximation term that simplifies finding a solution. Smoothed linear programs can be represented as:
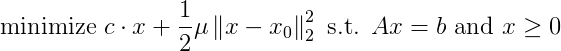
A smoothed linear program can be solved in TFOCS for Spark using a helper function as follows:
A complete Linear Programming example is presented here.
Get started with ETL
Implementation
The implementation of TFOCS for Spark closely follows that of the Matlab TFOCS package. We’ve ensured that all of the functionality in TFOCS for Spark can be easily traced back to the corresponding code in the original Matlab TFOCS implementation.
TFOCS for Spark includes a general purpose optimizer with an implementation that is independent of whatever distributed data storage format is employed during optimization. This means that the same optimizer code runs whether operating on a row matrix or a block matrix, for example. Once some basic operations are implemented for a new storage format, the optimizer “just works” for data in that format.
What’s next?
We’ve implemented some key features in the initial version of TFOCS for Spark, but there’s more work to be done. We would love to see support for additional data storage formats (for example block matrix storage), sparse vectors, and new objective functions. Contributions from the open source community are both welcome and encouraged.
Acknowledgements
As the developer of TFOCS for Spark, I would first like to thank Databricks for supporting this project. I am also immensely grateful to Xiangrui Meng and Reza Zadeh for their guidance during the design and development of TFOCS for Spark. I began working with Spark by submitting small patches as a rookie open source contributor, and since then my involvement with Spark has led to both intellectually rewarding projects and new professional opportunities. I encourage any readers with even a passing interest in Spark hacking to pull out their favorite editor and give it a try!
